Fibonacci Sequence of Numbers

Fibonacci Sequence & Phi (Φ)

 

The Fibonacci Sequence: A Mathematical Legacy

 

The Fibonacci sequence, named after the Italian mathematician Leonardo of Pisa—better known as Fibonacci (c. 1170–1240)—is a cornerstone of mathematics with profound applications in the natural sciences. The Fibonacci sequence illustrates how simple recursive rules can give rise to intricate and complex patterns, creating a remarkable bridge between pure mathematics, biology, art, and computer science. It continues to stand as a timeless symbol of mathematical elegance found throughout the natural world.

Historical Background

• Fibonacci introduced this sequence to Western audiences in his influential 1202 work Liber Abaci, using it to model the theoretical growth of a rabbit population.
• The Fibonacci sequence was already known in Indian mathematics, where it appeared in the context of Sanskrit poetic meter. What made Fibonacci’s contribution significant was his connection of the sequence to the Hindu-Arabic numeral system.
  

 

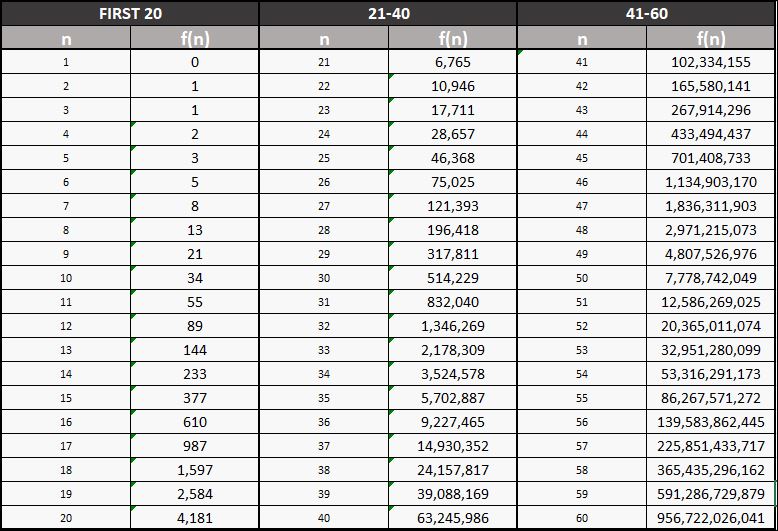
The Fibonacci Sequence of Numbers Explained

Fibonacci discovered a unique numerical sequence in which each number is the sum of the two preceding numbers. The sequence is defined recursively, as follows:

• 1+1=2

• 1+2=3

• 2+3=5

• 3+5=8

• 5+8=13

• 8+13=21

• 13+21=34

… to infinity

or else: F(n) = F(n-2) + F(n-1)

Table: The first 60 Fibonacci Numbers

 

Applications of Fibonacci Numbers:

• On a cosmic scale, spiral galaxies illustrate Fibonacci patterns
• In nature, examples include phyllotaxis (leaf and spiral arrangements in plants), sunflower seed patterns, and pinecones
• In all financial markets, Fibonacci numbers are used in technical analysis through retracements, extensions, and other tools
• In stock markets, indices and individual stock prices often find support and resistance near Fibonacci numbers.
• In computer science, they appear in efficient algorithms like Fibonacci heaps and dynamic programming techniques
• In architecture, they are evident in aesthetic proportions, such as those found in the Parthenon
• In art, Fibonacci patterns can be identified in paintings like the Mona Lisa

More about the Fibonacci Sequence in Nature: https://museum.cornell.edu/nature-and-math-the-fibonacci-sequence/

 

The Fibonacci Ratios

When you begin dividing Fibonacci numbers, the results consistently approach three key ratios: 1.618, 0.618, and 0.382. For example, take the Fibonacci numbers 144, 233, and 377:

• If you divide 233 by 144, the result is 1.618
• If you divide 144 by 233, the result is 0.618
• If you divide 144 by 377, the result is 0.382

These ratios—1.618, 0.618, and 0.382—are especially important in trading stocks, Forex, or other financial assets. Fibonacci ratios form the basis of a wide range of trading tools found in all modern trading platforms.

Moreover, the Fibonacci number sequence underpins various methodologies used in global market trading. Numerous theories and strategies explain market behavior based solely on Fibonacci numbers and their derived ratios. This sequence and its ratios are integral to hundreds of trading systems around the world.

---

 

Fibonacci Sequence of Numbers and Phi

 

As mentioned earlier, if we divide each Fibonacci number by the one preceding it, the result consistently approaches 1.618. This number, 1.618, is known as Phi (Φ) or else the Golden Ratio.

■ Phi (Φ) = 1.618033… (until infinity)

■ Golden Ratio Connection:

As n→∞, 

( Fn+1 / Fn ) ≈ ϕ ≈ 1.618

 

The Ancient Origins of Phi

The number Phi was formally defined by the ancient mathematician Euclid around 300 B.C. However, long before Euclid, the philosopher Plato (428 B.C. – 347 B.C.) regarded the Golden Ratio as the most universally binding of all mathematical relationships. Even earlier, the mathematician Pythagoras (570 B.C. – 475 B.C.) also referenced the Golden Ratio. In truth, no one knows exactly who first discovered Phi. Some believe the ancient Egyptians applied it in the construction of the Pyramids, while others credit the ancient Sumerians with its discovery.

• The symbol Phi (φ) was named in 1914 by the American mathematician Mark Barr in honor of Phidias
• Phidias (Greek: Φειδίας), the renowned ancient sculptor who created the statue of Zeus at Olympia, one of the seven wonders of the ancient world. He is believed to have used the Golden Ratio in the design of the Athenian Parthenon.

 

Unique mathematical properties of Phi

It is impossible to fully pin down the golden ratio. The first 10 million digits were computed in 1996, and no repeating pattern has ever been found. Here are some basic mathematical properties of Phi.

Key Properties of Phi:

(i) Squaring Phi (Φ²) gives Phi plus 1, or approximately 2.618, which means:

■ Φ² = Φ + 1 = 2.618

(ii) Dividing 1 by Phi (1/Φ) gives Phi minus 1, or approximately 0.618, which means:

■ 1 / Φ = Φ – 1 = 0.618

■ The value 0.618 is sometimes represented by a small ‘p’

 

Golden Spiral

A golden spiral in Geometry is a logarithmic spiral whose growth factor is Phi (Φ). Α golden spiral gets wider by a factor of Phi for every quarter turn it makes.

• Growth Factor: The golden spiral expands by a factor of φ ≈ 1.618 (the Golden Ratio) for every 90° (quarter turn) of rotation.

• Phi in Every Turn:

  • After 90° (π/2 radians): Radius grows by φ.

  • After 180° (π radians): Radius grows by φ² ≈ 2.618.

  • After 360° (2π radians): Radius grows by φ⁴ ≈ 6.854.

Image: Fibonacci Golden Spiral

More about the Golden Spiral: https://en.wikipedia.org/wiki/Golden_spiral

 

Cosmic Applications of Phi

• The diameters of the Moon and Earth form a geometric relationship close to Phi.
• The distances between the Sun and planets in our solar system closely follow powers of Phi.
• In 2003, NASA reported that the shape of the Milky Way resembles a dodecahedron based on Phi. The galaxy has several spiral arms, each forming a logarithmic spiral of about 12 degrees, matching the shape of the Golden Spiral.

 

Image: Two Golden Spirals applied to the nearby spiral galaxy M74 (Qexpert.com, original image: NASA/ESA Hubble Space Telescope)

---

 

Fibonacci Tools in Trading

 

Traders utilize ratios derived from the golden ratio (φ) to identify key price levels and timing in financial markets. The primary Fibonacci-based techniques include:

A. Fibonacci Retracements

• Purpose: To identify potential support and resistance levels during price corrections within a trend.
• Method: Horizontal lines are drawn at key Fibonacci ratios—typically 23.6%, 38.2%, 50%, and 61.8%—between a significant swing high and low. Among these, the 61.8% retracement level is especially noted for indicating strong potential reversal zones.

Example: In gold markets, prices often rebound near the 61.8% retracement level during bullish trends.

B. Fibonacci Extensions

• Purpose: To project future price targets beyond the current trend, often used for setting profit-taking levels.
• Common Extension Levels:

→ 161.8% (φ × 100%)

→ 261.8% (φ² × 100%)

→ 423.6% (φ³ × 100%)

Example: If a stock climbs from $100 to $150, a 161.8% extension projects a target of approximately $180:
($50 move × 1.618) + $150 = $180.90

C. Fibonacci Fans & Arcs

Fibonacci Fans: Diagonal lines drawn from a trend’s origin through price points divided by key ratios (38.2%, 50%, 61.8%). These serve as dynamic support and resistance levels as price evolves.

Fibonacci Arcs: Curved lines plotted using the same phi-based ratios, intersecting price action to mark potential reversal zones based on both time and price movement.

D. Fibonacci Time Zones

Method: Vertical lines are plotted at Fibonacci time intervals—1, 2, 3, 5, 8, etc.—from a significant price pivot. These intervals help forecast when major price moves or trend changes are more likely to occur.

---

 

■ Fibonacci Sequence and Phi (Φ)

George Protonotarios, Financial Analyst

for TradingFibonacci.com (c)