Guides

Trading with Fibonacci Mathematics
Fibonacci mathematics can help traders uncover the hidden proportionality in market behavior. Fibonacci extension analysis examines the extent of primary trends and countertrends to identify key reversal zones—levels where a trending market may lose momentum and reverse. » Fibonacci Sequence and Phi
Calculating the Basic Ratios Using the Fibonacci Sequence
The Fibonacci sequence begins as follows: 0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, etc. This sequence can be broken down into ratios. These Fibonacci ratios are derived by dividing one number in the sequence by another.
Excluding the initial numbers, we observe that:
✅ Every number is approximately 1.618 times the preceding number.
✅ Every number is approximately 0.618 of the number that follows it.
Note that 1.618 is known as the golden ratio, and its inverse is 0.618.
Key Ratios for Financial Trading
In financial trading, the key Fibonacci ratios are 0.236, 0.382, 0.618, 1.618, 2.618, and 4.236. Many traders also use 0.5 and 1.0.
Table: Key Fibonacci Ratios for Financial Trading
|
0.236 |
1.000 |
|
0.382 |
1.618 |
|
0.500 |
2.618 |
|
0.618 |
3.618 |
|
0.786 |
4.236 |
The Fibonacci sequence produces useful trading tools such as Fibonacci Retracement and Fibonacci Extensions.
eBook: Trading World Markets Using Phi and the Fibonacci Numbers
The Complete Guide to Fibonacci Trading and Phi by George M. Protonotarios
 The complete guide to Fibonacci trading and Phi, with references to Elliott Waves, Dow Theory, Gann Numbers, and Harmonic Patterns, designed for successful trading in the global financial markets—including Forex currencies, stocks, indices, metals, and energies.
The complete guide to Fibonacci trading and Phi, with references to Elliott Waves, Dow Theory, Gann Numbers, and Harmonic Patterns, designed for successful trading in the global financial markets—including Forex currencies, stocks, indices, metals, and energies.
► Find the Book at Amazon (ePub) | ► Find the book in .PDF
Introduction to the "Trading World Markets" Book
This book covers a wide range of trading theories and methodologies involving Fibonacci numbers and their applications. It includes all the basic Fibonacci trading practices and tools based on Fibonacci ratios. Phi and Fibonacci numbers are not just another technical analysis tool; Phi proportions appear everywhere—in art, architecture, the spiral of our DNA, and even in natural plant formations.
The first chapter explores the mathematical properties of Phi and its applications beyond financial markets. The following chapters cover Dow Theory, Elliott Wave Theory, and Gann numbers. At the end of each chapter, you’ll discover how these theories relate to Fibonacci numbers. You’ll also learn how to use Fibonacci numbers to create a trading system based on Fibonacci Moving Averages (MAs). Additionally, the book explains popular Fibonacci tools such as Fibonacci Retracement, Fibonacci Extension, and Fibonacci Fan. Two chapters focus on Harmonic Trading and Harmonic Patterns—one of the most advanced trading techniques, entirely based on Fibonacci proportions. Six basic harmonic patterns are detailed, with their properties and chart examples. The final chapter discusses money management and how the irrational brain affects our daily decision-making.
INTRODUCTION
- CHAPTERS:
- THE ORIGINS OF FIBONACCI NUMBERS AND PHI (Φ)
- THE DOW THEORY AND FIBONACCI NUMBERS
- THE ELLIOTT WAVE THEORY AND FIBONACCI NUMBERS
- W. D. GANN AND FIBONACCI NUMBERS
- FIBONACCI NUMBERS AND MOVING AVERAGES
- FIBONACCI RETRACEMENT AND OTHER TOOLS
- INTRODUCTION TO HARMONIC TRADING
- SIX HARMONIC PATTERNS
- THE IRRATIONAL BRAIN & MONEY MANAGEMENT
- APPENDIX
- Dow Jones Industrial Record Highs
- Heikin-Ashi Charts
By combining the information and tools presented throughout the chapters, you have the opportunity to build the foundation of a trading system out of chaos—a system that can help you become less emotional when trading the global markets and significantly improve your chances of winning.
► Find the Book at Amazon | ► Find the book in .PDF
■ Trading World Markets Using Phi and the Fibonacci Numbers
TradingFibonacci.com
▶️ FIND OUT MORE AT TRADINGFIBONACCI.COM
Fibonacci Sequence & Phi (Φ)
The Fibonacci Sequence: A Mathematical Legacy
The Fibonacci sequence, named after the Italian mathematician Leonardo of Pisa—better known as Fibonacci (c. 1170–1240)—is a cornerstone of mathematics with profound applications in the natural sciences. The Fibonacci sequence illustrates how simple recursive rules can give rise to intricate and complex patterns, creating a remarkable bridge between pure mathematics, biology, art, and computer science. It continues to stand as a timeless symbol of mathematical elegance found throughout the natural world.
Historical Background
- Fibonacci introduced this sequence to Western audiences in his influential 1202 work Liber Abaci, using it to model the theoretical growth of a rabbit population.
- The Fibonacci sequence was already known in Indian mathematics, where it appeared in the context of Sanskrit poetic meter. What made Fibonacci’s contribution significant was his connection of the sequence to the Hindu-Arabic numeral system.
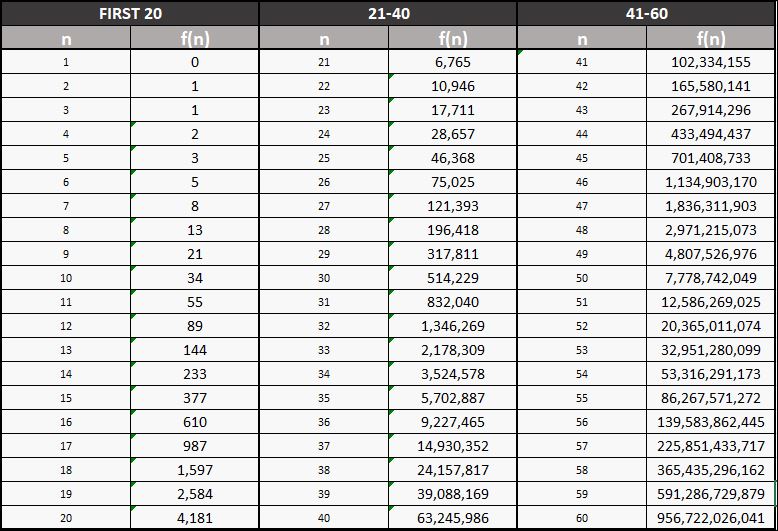
The Fibonacci Sequence of Numbers Explained
Fibonacci discovered a unique numerical sequence in which each number is the sum of the two preceding numbers. The sequence is defined recursively, as follows:
-
1+1=2
-
1+2=3
-
2+3=5
-
3+5=8
-
5+8=13
-
8+13=21
-
13+21=34
… to infinity
or else: F(n) = F(n-2) + F(n-1)
Table: The first 60 Fibonacci Numbers
Applications of Fibonacci Numbers:
- On a cosmic scale, spiral galaxies illustrate Fibonacci patterns
- In nature, examples include phyllotaxis (leaf and spiral arrangements in plants), sunflower seed patterns, and pinecones
- In all financial markets, Fibonacci numbers are used in technical analysis through retracements, extensions, and other tools
- In stock markets, indices and individual stock prices often find support and resistance near Fibonacci numbers.
- In computer science, they appear in efficient algorithms like Fibonacci heaps and dynamic programming techniques
- In architecture, they are evident in aesthetic proportions, such as those found in the Parthenon
- In art, Fibonacci patterns can be identified in paintings like the Mona Lisa
More about the Fibonacci Sequence in Nature: https://museum.cornell.edu/nature-and-math-the-fibonacci-sequence/
The Fibonacci Ratios
When you begin dividing Fibonacci numbers, the results consistently approach three key ratios: 1.618, 0.618, and 0.382. For example, take the Fibonacci numbers 144, 233, and 377:
- If you divide 233 by 144, the result is 1.618
- If you divide 144 by 233, the result is 0.618
- If you divide 144 by 377, the result is 0.382
These ratios—1.618, 0.618, and 0.382—are especially important in trading stocks, Forex, or other financial assets. Fibonacci ratios form the basis of a wide range of trading tools found in all modern trading platforms.
Moreover, the Fibonacci number sequence underpins various methodologies used in global market trading. Numerous theories and strategies explain market behavior based solely on Fibonacci numbers and their derived ratios. This sequence and its ratios are integral to hundreds of trading systems around the world.
Fibonacci Trading

Uncovering the hidden proportions underlying market behavior...
🎯 Explore Fibonacci trading tools and tutorials:
» Combining Fibonacci with S&R
» Combining Fibonacci with TAs
» MT4 MT5 Fibonacci Indicators
📌 Discover the Advice from Market Gurus:
📖 eBOOK: TRADING WORLD MARKETS USING PHI AND THE FIBONACCI NUMBERS {by G. Protonotarios}
A Guide to Fibonacci Trading with Insights from Elliott Waves, Gann Numbers, and Harmonic Patterns..
► ePub at Amazon | ► PDF Version
Online Forex Brokers
Compare Online Brokers for International Traders: » Compare ECN/STP Brokers
Trading Education
2025 Holidays
 |
|
| Date | Holiday |
| Jan. 1, Wednesday, | New Year’s Day |
| Jan. 20, Monday | Martin Luther King |
| Feb. 17, Monday | Presidents' Day |
| April 18, Friday | Good Friday |
| May 26, Monday | Memorial Day |
| June 19, Thursday, | Juneteenth Day |
| July 4, Friday | Independence Day |
| Sept. 1, Monday | Labor Day |
| Nov. 27, Thursday | Thanksgiving Day |
| Dec. 25, Thursday | Christmas Day |
Chart Patterns

📊 Identify and Trade High-Probability Chart Patterns:
» Time Frames and Trading Styles

📈 Engaging in Global Market Trading